1. LSM Tree 简介

在具体进入本实验之前，我们先来简单介绍LSM Tree。

LSM Tree是一种KV存储架构。其核心思想是，将KV存储的数据以SSTable的形式进行持久化，并通过MemTable进行内存缓存，当MemTable的数据量达到一定阈值时，将其持久化到磁盘中，并重新创建一个MemTable。LSM Tree的核心思想是，将KV存储的数据以SSTable的形式进行持久化，并通过MemTable进行内存缓存。并且，数据以追加写入的方式进行，删除数据也是通过更新的数据进行覆盖的方式实现。

Fig 1

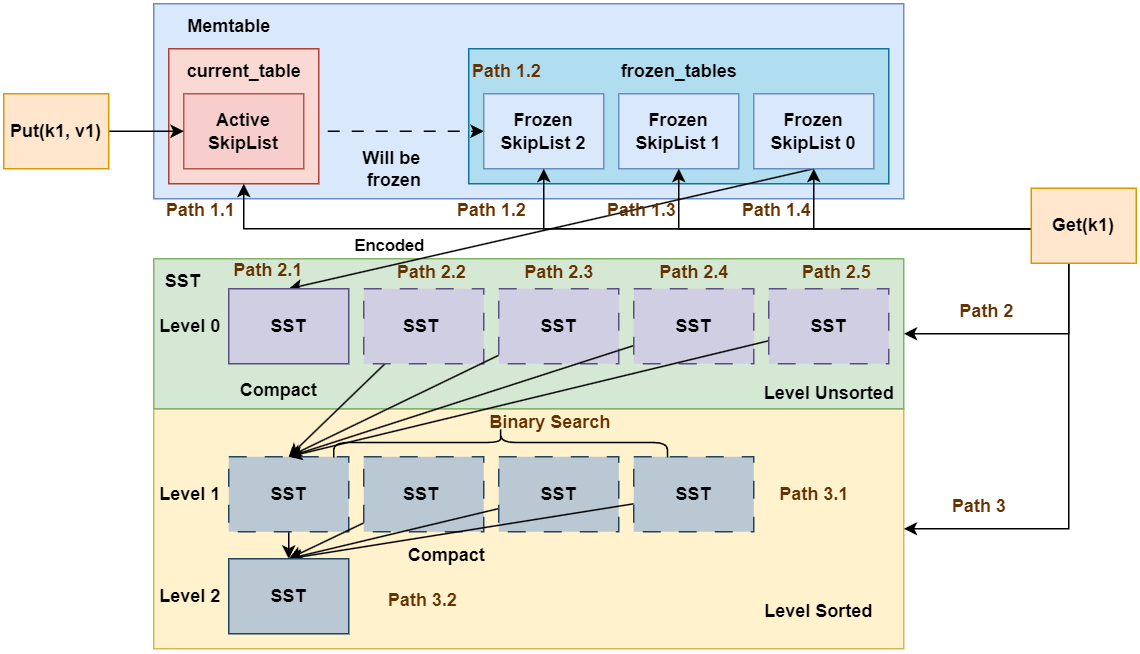
如图所示为LSM Tree的核心架构。我们通过Put, Remove和Get操作的流程对其进行介绍。

1.1 Put 操作流程

Put操作流程如下：

将Put操作的数据写入MemTable中
1. MemTable中包括多个键值存储容器(本项目是采用的跳表SkipList)
  1. 其中有一份称为current_table, 即活跃跳表, 其可读可写
  2. 其余的多份跳表均为frozen_tables, 即即冻结跳表, 其只能进行读操作
2. Put的键值对首先插入到current_table中
  1. 如果current_table的数据量未达到阈值, 直接返回给客户端
  2. 如果current_table的数据量达到阈值, 则将current_table被冻结称为frozen_tables中的一份, 并重新初始化一份current_table
如果前述步骤导致了新的frozen_table产生, 判断frozen_table的容量是否超出阈值
如果超出阈值, 则将frozen_table持久化到磁盘中, 形成SST(全程是Sorted String Table), 单个SST是有序的。
1. SST按照不同的层级进行划分, 内存中的MemTable刷出的SST位于Level 0, Level 0的SST是存在重叠的。（例如SST 0的key范围是[0, 100), SST 1的key范围是[50, 150), 那么SST 0和SST 1的key在50, 100)范围是重叠的, 因此无法在整个层级进行二分查询）
2. 当Level 0的SST数量达到一定阈值时, 会进行Level 0的SST合并, 将SST进行compact操作, 新的SST将放在Level 1中。同时，为保证此层所有SST的key有序且不重叠, compact的SST需要与原来Level 1的SST进行重新排序。由于compact时将上一层所有的SST合并到了下一层, 因此每层单个SST的容量是呈指数增长的。
3. 当每一层的SST数量达到一定阈值时, compact操作会递归地向下一层进行。

1.2 Remove 操作流程

由于LSM Tree的操作是追加写入的, 因此Remove操作与Put操作本质上没有区别, 只是Remove的value被设定为空以标识数据的删除。

1.3 Get 操作流程

Get操作流程如下:

先在Memtable中查找, 如果找到则直接返回。
1. 优先查找活跃跳表current_table
2. 其次尝试查找frozen_tables, 按照id倒序查找(因为id越小, 表示SkipList越旧)
如果在Memtable中未找到, 则在SST中查找。
1. 先在Level 0层查找, 如果找到则直接返回。注意的是, Level 0层不懂的SST没有进行排序, 因此需要按照SST的id倒序逐个查找(因为id越小, 表示SST越旧, 优先级越低)
2. 随后逐个在后面的Level层查找, 此时所有的SST都已经进行过排序, 因此可在Level层面进行二分查询。
如果SST中为查询到, 返回。

至此，你对LSM Tree的CRUD操作流程有了一个初步的印象, 如果你现在看不懂的话, 没关系。后续的Lab中会对每个模块有详细的讲解。

2. LSM Tree VS B-Tree

接下来对比分析一下LSM Tree 和 B-Tree。B-Tree 和 LSM-Tree 是两种最常用的存储数据结构，广泛应用于各种数据库和存储引擎中。

2.1 B-Tree 概述

2.1.1 基本结构

B-Tree 是一种多路平衡搜索树，具有如下特点：

多路搜索：每个节点可包含多个 key 和多个指向子节点的指针，典型的阶为 M 的 B-Tree 每个节点最多包含 M-1 个 key 和 M 个子指针。
有序性：节点内的 key 是有序排列的，满足搜索树的性质（左子树所有 key 小于当前 key，右子树所有 key 大于当前 key）。
节点平衡：B-Tree 总是保持所有叶子节点在同一深度，避免了不平衡树造成的性能劣化。
磁盘优化：B-Tree 节点设计与磁盘页大小（如 4KB）对齐，尽量减少 I/O 次数。一个节点一般映射为一个磁盘页。

2.1.2 操作流程

查找操作

从根节点开始，顺序查找当前节点内的 key；
若找到对应 key，返回其值；
若未找到，确定 key 所属范围并跳转到对应子节点；
重复上述步骤，直到叶子节点。

插入操作

先定位插入位置；
若目标页未满，直接插入；
若目标页已满，触发分裂操作，将节点拆分为两个，并将中间 key 上移至父节点；
如果父节点也满，则递归向上分裂，可能导致树高度加一。

删除操作（简略）

查找要删除的 key；
若为叶子节点直接删除，若为内部节点需用前驱/后继替换；
若删除导致节点 key 数小于最小值（通常是 M/2），需借 key 或合并兄弟节点，保持平衡。

2.1.3 性能特点

操作类型	时间复杂度	备注
查找	O(logₘN)	树高取决于扇出 M，M 越大树越矮
插入	O(logₘN)	最多向上分裂至根节点
删除	O(logₘN)	包含调整和合并操作

优势：查找路径短，适用于 OLTP 事务型数据库；
劣势：写入为页内更新和随机写，且可能导致写放大,不适合写密集型负载。

🌪️ “随机写”是什么意思？

在 B-Tree 中，每次写入（插入、更新或删除）都必须找到对应位置，比如一个叶子节点中的第 n 个 key：

B-Tree 会从根节点一路查找，定位到目标页（也就是磁盘上的一个节点）。

如果该页满了，还要分裂成两个页，再更新父节点指针，可能一直递归到根。

每一个操作，可能都要读写不同位置的磁盘页——这些页不在相邻磁盘位置上，就叫“随机写”。

而磁盘（特别是传统 HDD）最慢的操作就是随机写。

🔥 “写放大”又是什么？

你本来只是想写入一个 key-value 对，结果 B-Tree 却可能会因为：

页满而分裂；

父节点也满而再分裂；

更新多个索引路径节点；

导致你实际上要写入多个节点、多个页——一次小写入导致多次磁盘写入，这就叫写放大（Write Amplification）。

比如你写了 1KB 数据，磁盘实际写了 16KB，甚至 64KB，这种浪费，就是放大了。

MemTable（内存表）：所有写操作首先追加到内存中的有序结构（如跳表）。
SSTable（磁盘表）：当 MemTable 达到阈值时，将其定期刷新为只读的磁盘文件。
后台 Compaction（合并）：将多个旧的 SSTable 合并、去重，并生成新的 SSTable，控制文件数量与数据冗余。

2.2.3 优化手段

Bloom Filter：快速判断某 key 是否存在于某个 SSTable，减少不必要的磁盘查找。
Index Block / Block Cache：缓存热点数据页，加速读请求。
Tiered / Leveled Compaction：通过分层或分阶段合并，平衡写放大与读放大。

2.3. B-Tree vs. LSM-Tree 对比

特性	B-Tree	LSM-Tree
写入模式	随机写，页内更新，可能分裂节点	顺序写（追加），后台合并
写放大	较低	较高（受合并策略影响）
读取路径	单次树搜索	多级查找（MemTable + 多个 SSTable + 合并）
读写性能场景	读密集型	写密集型
磁盘友好性	随机 I/O	顺序 I/O，更适合 SSD

小结：LSM-Tree 在写入吞吐上优于 B-Tree，但读取延迟与 I/O 成本相对更高。更深入的对比分析可以阅读： https://tikv.org/deep-dive/key-value-engine/b-tree-vs-lsm/

2.4 常见系统及应用场景

存储引擎 / 数据库	类型
LevelDB	嵌入式 KV 存储引擎
RocksDB	KV 存储引擎
HyperLevelDB	分布式 KV 存储
PebbleDB	嵌入式 KV 存储
Cassandra	分布式列存储数据库
ClickHouse	分析型数据库
InfluxDB	时间序列数据库

2.5 LSM-Tree 优化研究

LSM Tree自1997年提出后，有很多研究人员在LSM Tree的基础上进行了改进，部分代表性工作比如：

RocksDB, LevelDB：经典的LSM Based KV存储引擎.

WiscKey: Separating Keys from Values in SSD-Conscious Storage：分离 Key 和 Value，降低写放大

Monkey: Optimal Bloom Filters and Tuning for LSM-Trees：优化布隆过滤器分配策略，减少读放大

这里不再进行详细介绍，感兴趣的可以阅读相关论文。

Tiny-LSM-Lab